今天北京高考在线整理了高中数学指数函数的图象和性质的应用3个必考题型解析，高三考生务必考前再做一遍~

一、必考点总结：

1、指数函数的定义域与值域

与指数函数有关的值域或最值问题，通常利用换元法，将其转化为两个基本初等函数的单调性或值域问题，注意换元过程中“元”的取值范围的变化．换元法与二次函数相结合是解决与指数函数有关的值域问题的常用方法．

2、指数函数图象恒过定点问题

定点是指图像不受参数影响恒过的点，指数函数图像恒过定点(0，1)，对于指数型函数令指数部分整体为0，即可求得定点．

3、指数函数比较大小问题

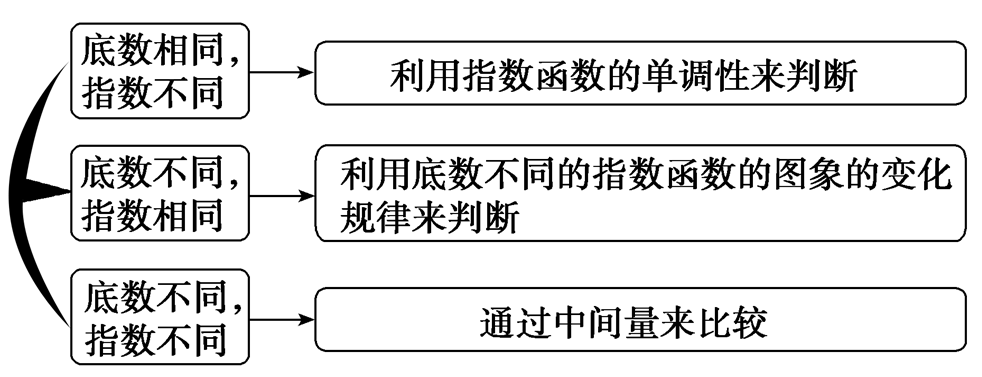
(1)同底数指数式比较大小的一般步骤：

①确定要考查的指数函数；

②由底数的范围确实指数函数的单调性；

③比较指数的大小，利用指数函数的单调性进行比较．

(2)同指数、底数不同的指数式比较大小，通常借助图像比较，注意底数对图像的影响．

(3)底数不同、指数也不相同时可借助中间值比较大小，通常将所要比较大小的数确定在两个整数之间，然后进行比较，指数式常借助0或1比较大小.

本考点在高考中常考查：(1)比较指数式的大小；(2)指数函数的图像与性质的应用；(3)以指数函数为载体，与其他函数、方程、不等式等知识的综合应用．以选择题和填空题为主，难度中等.

二、必考题型解析：

题型1　指数型函数的单调性

方法和技巧

函数y＝a^f(x)(a>0，a≠1)的单调性的处理技巧

(1)关于指数型函数y＝a^f(x)(a>0，且a≠1)的单调性由两点决定，一是底数a>1还是0<a<1；二是f(x)的单调性，它由两个函数y＝a^u，u＝f(x)复合而成．

(2)求复合函数的单调区间，首先求出函数的定义域，然后把函数分解成y＝f(u)，u＝φ(x)，通过考查f(u)和φ(x)的单调性，求出y＝f(φ(x))的单调性．

[对点训练]

题型2　指数型函数单调性的应用(应用型)

方法和技巧

1．比较指数式大小的3种类型及处理方法

2．指数不等式的两种类型

(1)形如a^x>a^b的不等式，借助函数y＝a^x(a>0，且a≠1)的单调性求解，如果a的取值不确定，需分a>1与0<a<1两种情况讨论；

(2)形如a^x>b的不等式，注意将b转化为以a为底数的指数幂的形式，再借助函数y＝a^x(a>0，且a≠1)的单调性求解．

[对点训练]

题型3　指数型函数的实际应用(应用型)

某城市现有人口总数为100万人，如果年自然增长率为1.2%，试解答下面的问题：

(1)写出该城市的人口总数y(万人)与年份x(年)的函数关系式；

(2)计算10年以后该城市人口总数(精确到0.1万人).

(参考数据：1.012⁹≈1.113，1.012¹⁰≈1.127)

解析：　(1)1年后该城市人口总数为：

y＝100＋100×1.2%＝100×(1＋1.2%)；

2年后该城市人口总数为：

y＝100×(1＋1.2%)＋100×(1＋1.2%)×1.2%

＝100×(1＋1.2%)²；

3年后该城市人口总数为：y＝100×(1＋1.2%)³；

……

x年后该城市人口总数为：y＝100×(1＋1.2%)^x.

(2)10年后该城市人口总数为：y＝100×(1＋1.2%)¹⁰

＝100×1.012¹⁰≈112.7(万人).

方法和技巧

解决指数型函数应用题的流程

(1)审题：理解题意，弄清楚关键字词和字母的意义，从题意中提取信息．

(2)建模：据已知条件，列出指数函数的关系式．

(3)解模：运用数学知识解决问题．

(4)回归：还原为实际问题，归纳得出结论．

[对点训练]

某种产品的年产量为a，在今后m年内，计划使产量平均每年比上年增加p%.

(1)写出产量y随年数x变化的函数解析式；

(2)若使年产量两年内实现翻两番的目标，求p.

解析：　(1)设年产量为y，年数为x，则y＝a(1＋p%)^x，

定义域为{x|0≤x≤m，且x∈N^*}．

(2)翻两番即变为原来的4倍，由题意得y＝a(1＋p%)²＝4a，解得p＝100.