立体几何常用的答题技巧中，很多同学往往却拿不全分数，甚至部分基础薄弱但坚持学习的同学拿不了几分，对学习积极性来说是很大的挫败。所以，北京高考在线着重给大家总结了这两种常见大题的一般求法：

一、平行与垂直的证明

立体几何方面的大题，出现相对较多的是平行和垂直的证明，当然垂直证明一般难度大于平行的证明。对于这一块内容，我们简单介绍下，大家可以看一下。

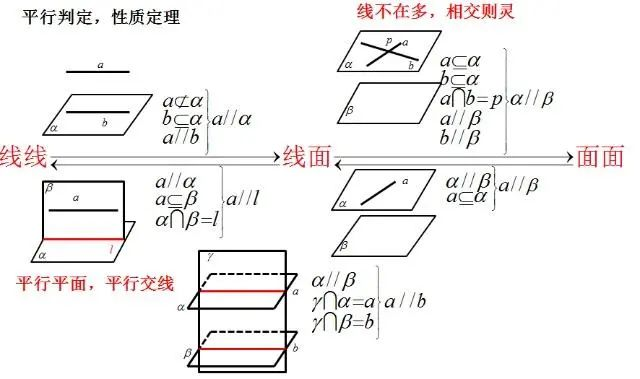
平行证明

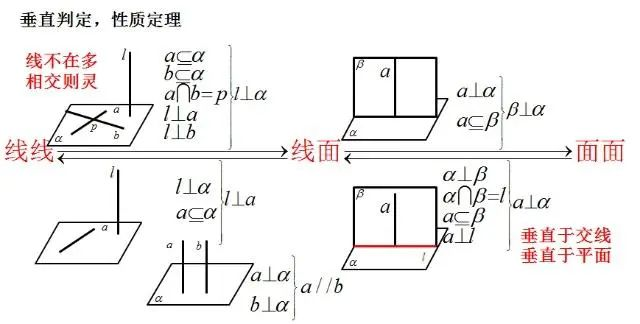
垂直证明

平行与垂直的证明，我们放在下一块求空间角时，分析大题目时一起分析。

二、求空间角

立体几何第二个经常出现的大题类型，基本都以求空间角的形式出现。求空间角主要分为三块内容：异面直线所成的角（线线角），线与面所成的角（线面角），面与面所成的角（二面角）。

首先，我们看一下考纲里面对空间角的要求：

A. 理解直线与平面所成角的概念，了解二面角及其平面角的概念．

B.了解求两直线夹角、直线与平面所成角、二面角的向量方法。

接下来我们分三点来分析空间角的求法：

1）异面直线所成的角（线线角）

定义：已知两条异面直线，经过空间任一点作直线，所成的角的大小与点的选择无关，把所成的锐角（或直角）叫异面直线所成的角（或夹角）。

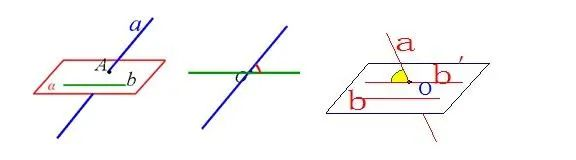
异面直线所成的角

求异面直线所成的角的方法：

1：平移，平移后使两条直线相交，求角；

2：向量法：建立坐标系，请求两条直线的坐标，利用公式。

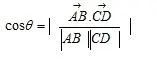
异面直线所成的角向量公式

典例分析——

例1．在正三棱锥S－ABC中，E为SA的中点，F为△ABC的中心，SA=BC=2，则异面直线EF与AB所成的角是 （ ）

（A）30° （B） 45° （C） 60° （D） 90°

例1答案

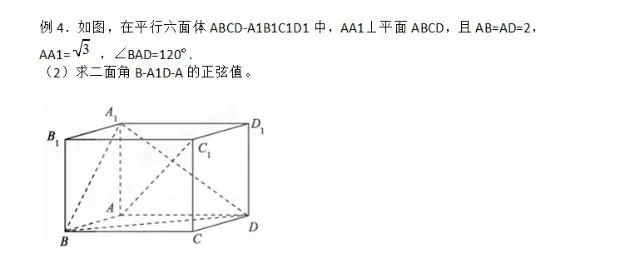
例2．如图，在平行六面体ABCD-A1B1C1D1中，AA1⊥平面ABCD，且AB=AD=2，AA1= 根号3，∠BAD=120.（1）求异面直线A1B与AC1所成角的余弦值；

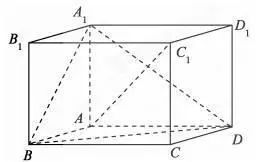
例2图

2）线与面所成的角（线面角）

1.线面角的定义：平面的一条斜线和它在平面上的射影所成的锐角叫做这条斜线和这个平面所成的角

2.求线面角的一般步骤：

（1）先找斜足

（2）经过斜线上一点作面的垂线（一般都是另一个端点），即作出垂足，连接斜足和垂足，找出线面角。

注意：做垂线时都是做线的垂线，然后证明是面的垂线。

3.向量法：

线面角

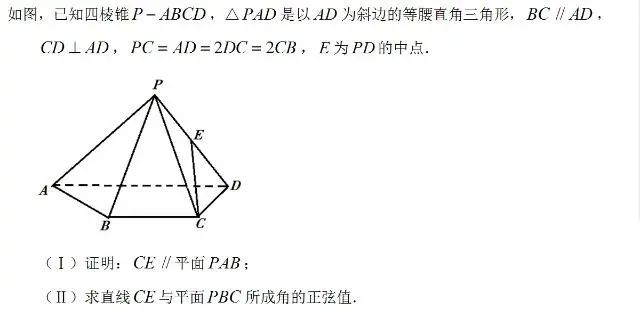
例3.

3）面与面所成的角（二面角）

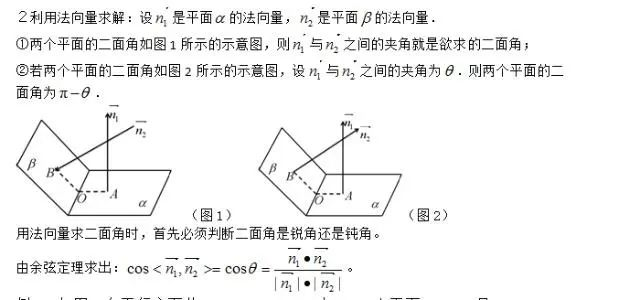
（1）过二面角的棱上的一点O分别在两个半平面内作棱的两条垂线OA,OB，角AOB则叫做二面角的平面角。

二面角的平面角的特点：

1.角的顶点在棱上 2.角的两边分别在两个面内 3.角的边都要垂直于二面角的棱。

声明：本文由北京高考在线团队（微信公众号：bjgkzx）排版编辑，内容来源于网络，如有侵权，请及时联系管理员删除。