2023年第十八届中国北方数学奥林匹克由中国数学奥林匹克北方培训中心主办。本届竞赛组委会业已成立，经组委会研究决定：第十八届中国北方数学奥林匹克定于2023年8月8---10日举行。本届赛事将通过线下和线上相结合的方式举办。北京高考在线整理了2023北方数学奥林匹克试题和解析，供考生参考。

2023北方数学奥林匹克试题和解析

第一题：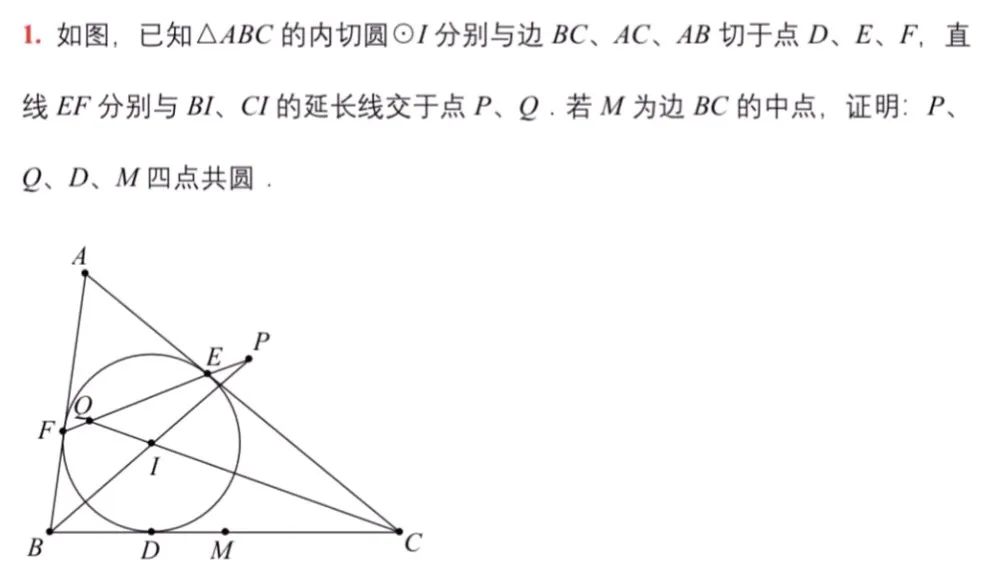

显然有FQBD共圆，DEPC共圆，

延长FE交BC于点T,

则TE·TF=TD²，TF·TQ=TB·TD,TE·PT=TD·TC,

所以PT·TQ=TB·TC=TD·TM（TDBC调和点列）.

综上可知证毕。

第二题：

分析：经过一些摸索，或者直接凭经验和感觉大胆猜测也可以。

解答：

首先取a1=a2=··=a（n–1）=0，a（n）=1/n，

此时因x（n）≥1/n，原式=1-1/n，是定值。

所以λ≤1-1/n。

另一方面考虑两组x序列：

（0，0··，1）和（1/n，1/n··，1/n）

由绝对值不等式容易知道两者中必有一个大于等于1-1/n，于是λ≥1-1/n。

综上，λ=1-1/n。

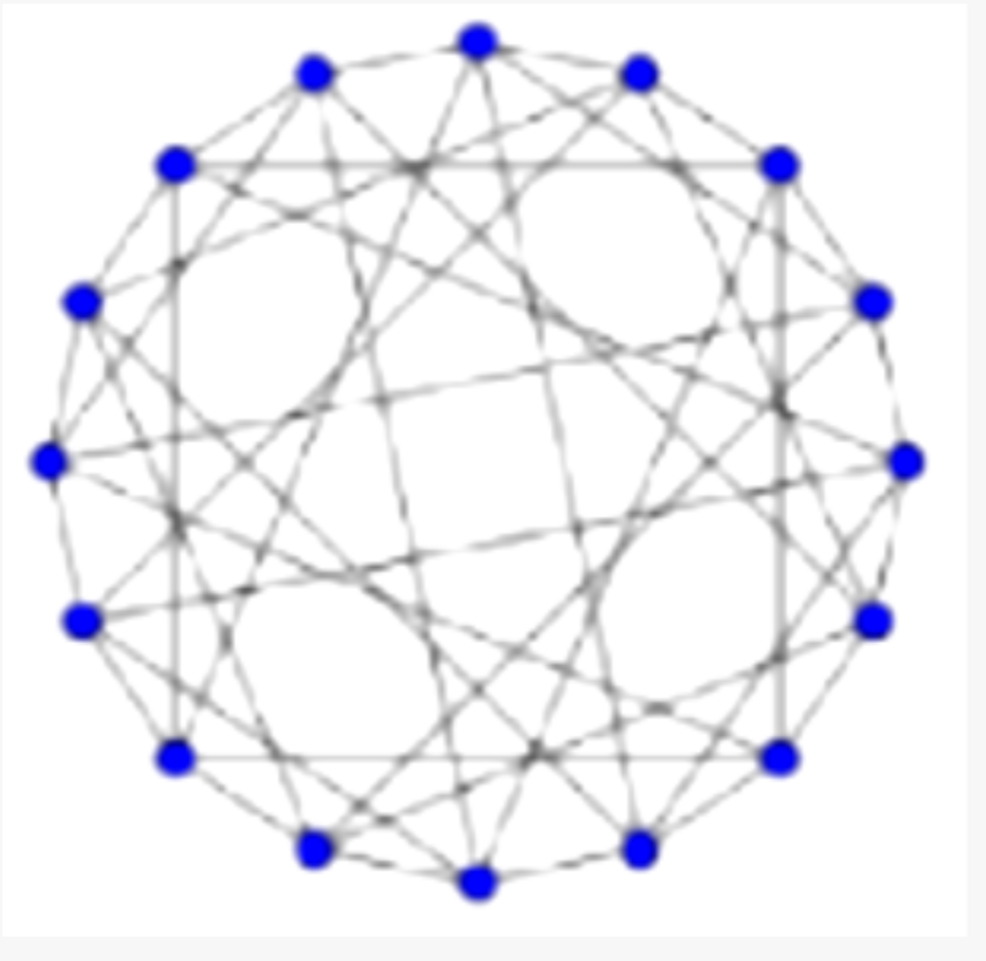
第三题：

当n=17时，对于一个点连出的16条边，一共染三种颜色，必然有6条边是同色的，对于这个6个点，两两连线只能是二染色的，其中一个点连出的5条边又有3条同色，于是必然有同色三角形。

当n=16时，可以构造出来。

第四题：

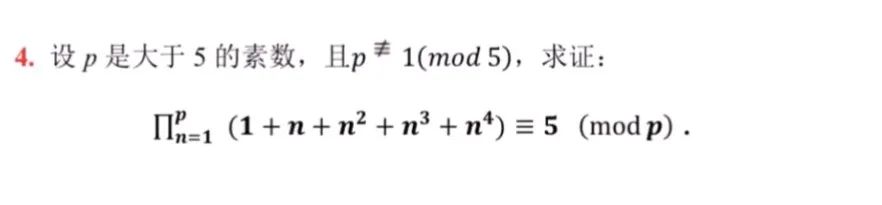
只需证明不存在x，y使得：

p不整除x–y且p整除x^5–y^5，

由费马小定理以及5不是p–1的因数证毕。

声明：本文由北京高考在线团队（微信公众号：bjgkzx）排版编辑，内容来源于竞赛与自招，如有侵权，请及时联系管理员删除。