由CCF主办、绍兴市第一中学承办的第42届全国青少年信息学奥林匹克竞赛(CCF NOI2025)将于2025年7月12日-18日在浙江绍兴举行。本文整理了第42届信息学奥林匹克竞赛NOI2025第一天试题,供考生参考。
相关汇总:2025年高中五大学科奥林匹克竞赛通知、试题及获奖名单汇总
免费福利:
为了方便考生更好备考五大学科竞赛,北京高考在线团队为大家整理了
《高中五大学科竞赛规划备考全攻略》电子版资料
https://www.gaokzx.com/form?xyppid=558524326727388226
《近十年高中竞赛试题集》电子版资料,可以直接打印练习!
免费领取:https://www.gaokzx.com/form?xyppid=558532509428616258
为了帮助同学们备考,北京高考在线团队为大家准备了五大学科竞赛交流分享群,
扫描下方二维码进群⬇️

第42届信息学奥林匹克竞赛NOI2025第一天试题
PART.01 [NOI 2025] 机器人
题目描述
NOI2025 正在绍兴举办,小 Y 为闭幕式表演制作了一个机器人并打算操控它从仓库走到礼堂。
绍兴的道路系统可以简化为n个路口以及连接这些路口的m条单行道路,且每条道路有一定的长度。为了方便将道路系统录入机器人的芯片,小 Y 对每一个路口连接的所有道路进行了编号。具体而言,若有d条道路以路口x为起点,则这d条道路会被小 Y 按照某种顺序编号为1∼d,分别称作以x为起点的第1∼d条道路。
小 Y 的机器人内部有一个参数p。给定参数p的上限k与修改费用v1,v2,…,vk−1,w2,w3,…,wk。小 Y 将按照如下规则设置与修改机器人的参数:
- 初始时,小 Y 将参数p设置为1。
- 在任意时刻,小 Y 可以远程控制机器人修改参数:
- 若p<k,则小 Y 可以花费vp的费用将p增加1,即p←p+1;
- 若p>1,则小 Y 可以花费wp的费用将p减少1,即p←p−1。
初始时,小 Y 的机器人位于机器人仓库,即路口1。当机器人位于路口x时,记以路口x为起点的第p条道路的终点为y,道路长度为z,则小 Y 可以花费z的费用操控机器人从x走到y。特别地,若以路口x为起点的道路不足p条,则小 Y 无法操控机器人走动。
小 Y 并不知道闭幕式表演所在的礼堂位于哪个路口,因此他需要对每个路口都做好准备。请你帮助他求出将机器人从仓库移动到每个路口所需费用的最小值。
输入格式
输入的第一行包含一个非负整数c,表示测试点编号。c=0表示该测试点为样例。
输入的第二行包含三个正整数n,m,k,分别表示路口数量、道路数量与参数p的上限。
输入的第三行包含k−1个非负整数v1,…,vk−1,表示增加参数p的费用。
输入的第四行包含k−1个非负整数w2,…,wk,表示减少参数p的费用。
输入的第i+4(1≤i≤n)行包含若干个正整数,其中第一个非负整数di表示以路口i为起点的道路数量,接下来2di个正整数yi,1,zi,1,yi,2,zi,2,…,yi,di,zi,di,表示以路口i为起点的道路,其中yi,j,zi,j(1≤j≤di)分别表示编号为j的道路的终点与长度。
输出格式
输出一行n个整数,其中第i(1≤i≤n)个数表示小 Y 将机器人从仓库移动到路口i所需费用的最小值。特别地,若小 Y 无法将机器人从仓库移动到该路口,则输出−1。
输入输出样例
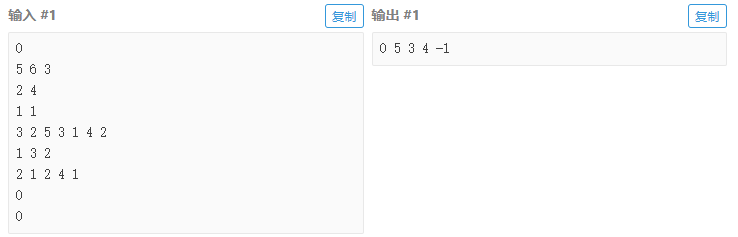
说明/提示
样例 1 解释
小 Y 可以按照以下方案将机器人分别从仓库移动到路口1∼4:
- 对于路口1:小 Y 的机器人初始时即位于路口1,因此所需费用为0。
- 对于路口2:小 Y 操控机器人沿以路口1为起点的第1条道路走到路口2,所需费用为5。
- 对于路口3:小 Y 将参数p增加1,然后操控机器人沿以路口1为起点的第2条道路走到路口3,所需费用为2+1=3。
- 对于路口4:小 Y 将参数p增加1,然后操控机器人沿以路口1为起点的第2条道路走到路口3,再操控机器人沿以路口3为起点的第2条道路走到路口4,所需费用为2+1+1=4。
可以证明,上述移动方案的所需费用均为最小值。
- 对于路口5:由于小 Y 无法将机器人移动到路口5,因此输出−1。
样例 2
见选手目录下的robot/robot2.in与robot/robot2.ans。
该样例满足测试点3∼5的约束条件。
样例 3
见选手目录下的robot/robot3.in与robot/robot3.ans。
该样例满足测试点6∼8的约束条件。
样例 4
见选手目录下的robot/robot4.in与robot/robot4.ans。
该样例满足测试点9,10的约束条件。
样例 5
见选手目录下的robot/robot5.in与robot/robot5.ans。
该样例满足测试点16∼18的约束条件。
数据范围
对于所有测试数据,保证:
- 1≤n,m≤3×105,1≤k≤2.5×105;
- 对于所有1≤i≤k−1,均有0≤vi≤109;
- 对于所有2≤i≤k,均有0≤wi≤109;
- 对于所有1≤i≤n,均有0≤di≤k,且∑i=1ndi=m;
- 对于所有1≤i≤n,1≤j≤di,均有1≤yi,j≤n,1≤zi,j≤109。
| 测试点编号 | n,m≤ | k≤ | 特殊性质 |
|---|---|---|---|
| 1,2 | 6 | 6 | C |
| 3∼5 | 103 | 103 | C |
| 6∼8 | 5×104 | 102 | 无 |
| 9,10 | 105 | 105 | AB |
| 11,12 | 105 | 105 | A |
| 13∼15 | 105 | 105 | C |
| 16∼18 | 105 | 105 | 无 |
| 19,20 | 3×105 | 2.5×105 | 无 |
- 特殊性质 A:保证v1=v2=⋯=vk−1=0且w2=w3=⋯=wk=0。
- 特殊性质 B:保证对于所有1≤i≤n,1≤j≤di,均有zi,j=1。
特殊性质 C:保证至多存在 10 个i满足di≥10。
PART.02[NOI 2025]序列变换
给定两个长度为n的整数序列B=[b1,…,bn],C=[c1,…,cn]。对于长度为n的非负整数序列D=[d1,…,dn],设S(D)为所有满足di=0的下标i的集合,定义f(D)=∑i∈S(D)bi,g(D)=∏i∈S(D)ci。特别地,若S(D)为空,则f(D)=0,g(D)=1。
小 L 有一个长度为n的正整数序列A=[a1,…,an]。小 L 可以对序列A做如下修改:
- 选择序列A的两个相邻的下标i,j(即1≤i,j≤n且∣i−j∣=1),若ai≤aj,则将aj改为aj−ai,同时将ai改为0。
小 L 可以进行任意多次修改操作,也可以不进行任何修改。对于所有序列A通过以上修改操作可以得到的序列D,小 L 想求出f(D)的最大值以及g(D)之和,请你帮助他求出这两个值。形式化地,记T(A)为序列A通过以上修改操作可以得到的所有序列的集合,你需要求出maxD∈T(A)f(D)以及∑D∈T(A)g(D)。其中,由于∑D∈T(A)g(D)可能较大,你只需要求出其对1,000,000,007取模后的结果。
输入格式
本题包含多组测试数据。
输入的第一行包含两个非负整数c,t,分别表示测试点编号与测试数据组数。c=0表示该测试点为样例。
接下来依次输入每组测试数据,对于每组测试数据:
- 第一行包含一个正整数n,表示序列长度。
- 第二行包含n个正整数a1,…,an,表示序列A。
- 第三行包含n个整数b1,…,bn,表示序列B。
- 第四行包含n个正整数c1,…,cn,表示序列C。
输出格式
对于每组测试数据,仅输出一行,其中包含两个整数,分别表示maxD∈T(A)f(D)以及∑D∈T(A)g(D)对1,000,000,007取模后的结果。注意:maxD∈T(A)f(D)不需要对1,000,000,007取模。
本题包含两个小问,正确回答其中任意一个小问均可获得部分分数。具体评分规则请参见【评分方式】。
输入输出样例
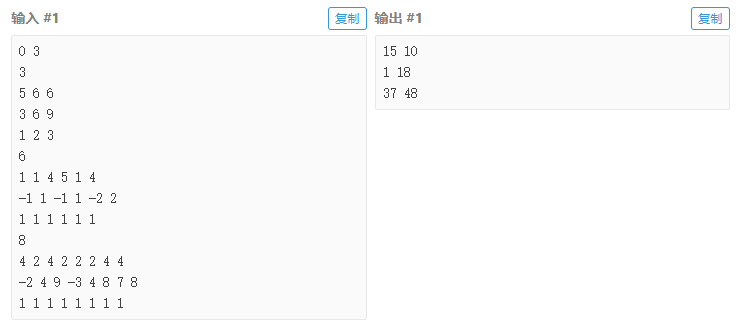
说明/提示
样例 1 解释
该样例共包含三组测试数据。
对于第一组测试数据,可以得到以下 4 个序列:
- D=[5,6,6],f(D)=0,g(D)=1;
- D=[0,1,6],f(D)=3,g(D)=1;
- D=[5,0,0],f(D)=6+9=15,g(D)=2×3=6;
- D=[0,0,5],f(D)=3+6=9,g(D)=1×2=2。
故maxD∈T(A)f(D)=max{0,3,15,9}=15,∑D∈T(A)g(D)=1+1+6+2=10。
样例 2
见选手目录下的sequence/sequence2.in与sequence/sequence2.ans。
该样例满足测试点 3、4 的约束条件。
样例 3
见选手目录下的sequence/sequence3.in与sequence/sequence3.ans。
该样例满足测试点 5、6 的约束条件。
样例 4
见选手目录下的sequence/sequence4.in与sequence/sequence4.ans。
该样例满足测试点 7 的约束条件。
样例 5
见选手目录下的sequence/sequence5.in与sequence/sequence5.ans。
该样例满足测试点 11、12 的约束条件。
样例 6
见选手目录下的sequence/sequence6.in与sequence/sequence6.ans。
该样例满足测试点16∼18的约束条件。
设N为单个测试点内所有测试数据的n的和。对于所有测试数据,保证:
- 1≤t≤20;
- 1≤n≤5,000,N≤4×104;
- 对于所有1≤i≤n,均有1≤Ai≤109;
- 对于所有1≤i≤n,均有−109≤Bi≤109;
- 对于所有1≤i≤n,均有1≤Ci≤109。
| 测试点编号 | n≤ | N≤ | 特殊性质 |
|---|---|---|---|
| 1,2 | 8 | 102 | 无 |
| 3,4 | 200 | 400 | B |
| 5,6 | 200 | 400 | 无 |
| 7 | 500 | 103 | A |
| 8∼10 | 500 | 103 | B |
| 11,12 | 500 | 103 | 无 |
| 13 | 3500 | 3×104 | A |
| 14,15 | 3500 | 3×104 | B |
| 16∼18 | 3500 | 4×104 | 无 |
| 19,20 | 5000 | 4×104 | 无 |
- 特殊性质 A:保证A1=A2=⋯=An=1。
- 特殊性质 B:保证对于所有1≤i≤n,Ai均在[1,109]中独立均匀随机生成。
评分方式
对于每个测试点:
- 正确回答所有测试数据的maxD∈T(A)f(D),可获得该测试点40%的分数;
- 正确回答所有测试数据的∑D∈T(A)g(D)对1,000,000,007取模后的结果,可获得该测试点60%的分数。
注意:即使选手仅回答了其中一个问题,也需要按照输出格式输出两个整数,分别对应两个问题的答案。
PART.03[NOI 2025] 数字树
给定一棵4n−1个结点的二叉树,其中每个非叶结点都有恰好两个子结点。非叶结点编号为1到2n−1,叶子结点编号为2n到4n−1。初始时,每个叶子结点上都没有数字。
定义一个 DFS 序是优美的,当且仅当按该 DFS 序将所有标有数字的叶子结点上的数字拼成一个序列时,该序列可以通过若干次消除相邻相同数字的方式得到空序列。例如,在下图中,若叶子结点4,6上标有数字1,叶子结点5,7上标有数字2,则按 DFS 序[1,4,2,7,3,5,6]将所有标有数字的叶子结点上的数字拼成的序列为[1,2,2,1],可以通过消除相邻的2的方式得到[1,1],再通过消除相邻的1的方式得到空序列,因此该 DFS 序是优美的;而按 DFS 序[1,4,2,3,5,6,7]将所有标有数字的叶子结点上的数字拼成的序列为[1,2,1,2],无法通过若干次消除相邻相同数字的方式得到空序列,因此该 DFS 序不是优美的。
给定n次操作,第i(1≤i≤n) 次操作会选择两个没有数字的叶子结点,然后将这两个结点标上数字i。保证在每次操作后,存在至少一个优美的 DFS 序。你需要求出每次操作后的优美的 DFS 序的数量。由于答案可能较大,你只需要求出答案对1,000,000,007取模后的结果。
输入格式
输入的第一行包含一个非负整数c,表示测试点编号。c=0表示该测试点为样例。
输入的第二行包含一个正整数n,表示二叉树的结点个数为4n−1。
输入的第i+2(1≤i≤2n−1) 行包含两个正整数li和ri,分别表示结点i的左右子结点。保证i<li,ri≤4n−1,且所有的li,ri互不相同。
输入的第i+2n−1(1≤i≤n) 行包含两个正整数ai,bi,表示第i次操作选择的叶子结点的编号。保证2n≤ai,bi≤4n−1,且所有的ai,bi互不相同。
输出格式
输出n行,其中第i(1≤i≤n) 行包含一个非负整数,表示第i次操作后的优美的 DFS 序的数量对1,000,000,007取模后的结果。
输入输出样例
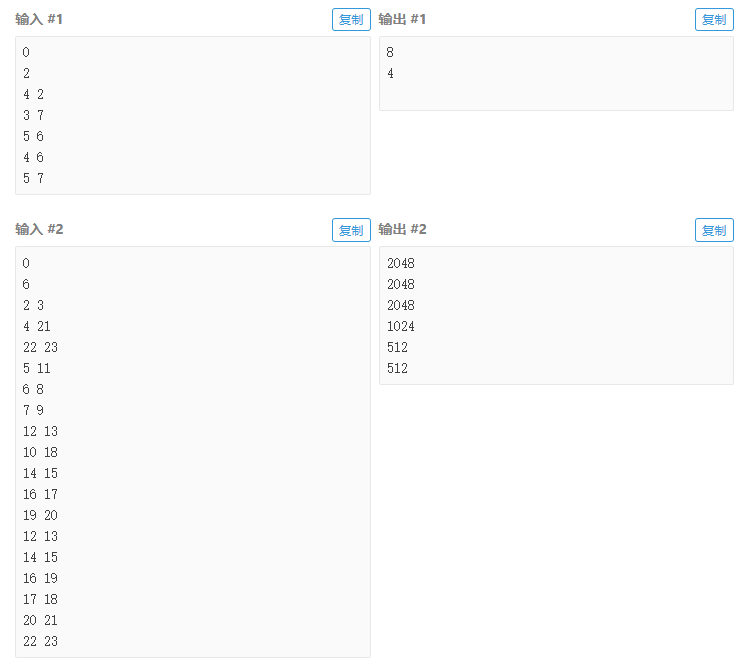
说明/提示
样例 1 解释
该样例即【题目描述】中所示的例子。
- 第一次操作后,叶子结点4和6上标有数字1,叶子结点5和7上没有数字,因此按任意 DFS 序拼成的序列均为[1,1],即所有的23=8个 DFS 序都是优美的。
- 第二次操作后,叶子结点4∼7上分别标有数字1,2,1,2,因此共有4个优美的 DFS 序,分别为[1,4,2,3,6,5,7],[1,4,2,7,3,5,6],[1,2,3,6,5,7,4],[1,2,7,3,5,6,4]。
样例 3
见选手目录下的tree/tree3.in与tree/tree3.ans。
该样例满足测试点6∼10的约束条件。
样例 4
见选手目录下的tree/tree4.in与tree/tree4.ans。
该样例满足测试点11,12的约束条件。
样例 5
见选手目录下的tree/tree5.in与tree/tree5.ans。
该样例满足测试点17∼20的约束条件。
样例 6
见选手目录下的tree/tree6.in与tree/tree6.ans。
该样例满足测试点24,25的约束条件。
数据范围
对于所有测试数据,保证:
- 1≤n≤2×105;
- 对于所有1≤i≤2n−1,均有i<li,ri≤4n−1,且所有的li,ri互不相同;
- 对于所有1≤i≤n,均有2n≤ai,bi≤4n−1,且所有的ai,bi互不相同;
- 在每次操作后,存在至少一个优美的 DFS 序。
| 测试点编号 | n≤ | 特殊性质 |
|---|---|---|
| 1,2 | 10 | 无 |
| 3∼5 | 102 | A |
| 6∼10 | 102 | 无 |
| 11,12 | 103 | A |
| 13,14 | 103 | 无 |
| 15,16 | 5×104 | AB |
| 17∼20 | 5×104 | B |
| 21,22 | 5×104 | 无 |
| 23 | 2×105 | A |
| 24,25 | 2×105 | 无 |
特殊性质 A:保证每次操作选择的两个叶子结点位于结点 1 的不同子树内。
特殊性质 B:保证存在非负整数m满足n=2m,且对于所有1≤i≤2n−1,均有li=2i,ri=2i+1。





































